4-th Runge Kutta Method 연습
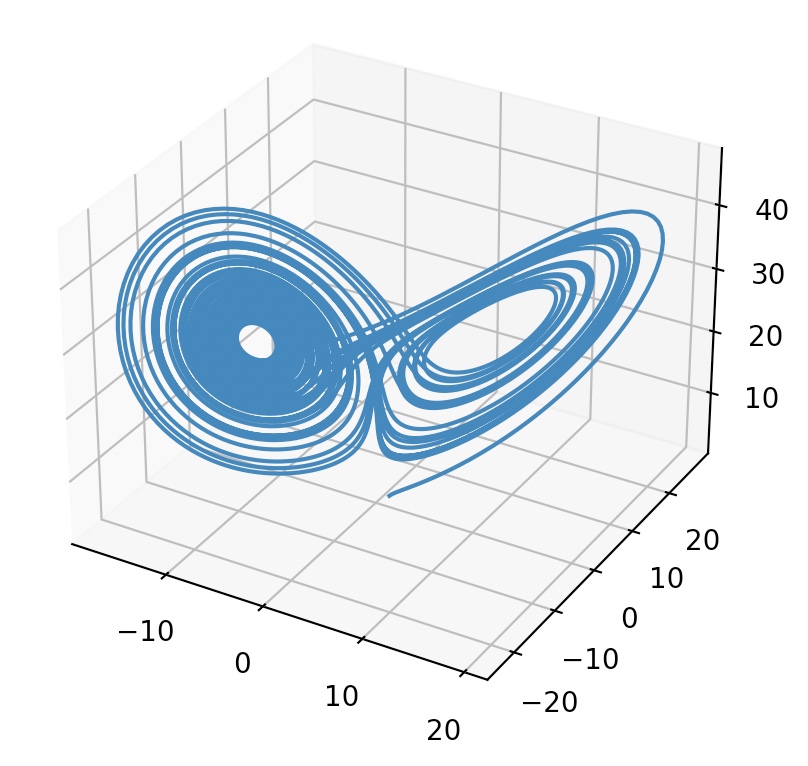
Lorenz Equation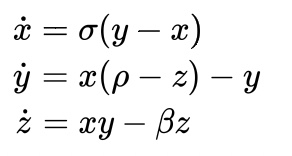
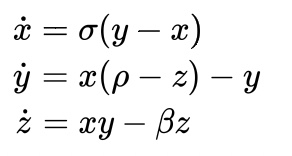
with sigma=10, beta=8/3, rho=28
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
def f(r, t): # dr/dt
x, y, z=r[0], r[1], r[2]
sigma=10.
rho=28.
beta=8/3
fx=sigma*(y-x)
fy=x*(rho-z)-y
fz=x*y-beta*z
return np.array([fx, fy, fz])
if __name__=="__main__":
t=np.linspace(0, 50, 10000)
dim=3
r=np.ones([len(t), dim])
k=np.zeros([4, dim], float) # Fourth Order Runge-Kutta Method
h=t[1]-t[0]
for i in range(1, len(t)): # Vector calculation
k[0]=h*f(r[i-1], t[i-1])
k[1]=h*f(r[i-1]+k[0]/2, t[i-1]+h/2)
k[2]=h*f(r[i-1]+k[1]/2, t[i-1]+h/2)
k[3]=h*f(r[i-1]+k[2], t[i-1]+h)
r[i]=r[i-1]+(k[0]+2*k[1]+2*k[2]+k[3])/6
fig=plt.figure()
ax=fig.gca(projection="3d")
ax.plot(r[:, 0], r[:, 1], r[:, 2] )
plt.show()
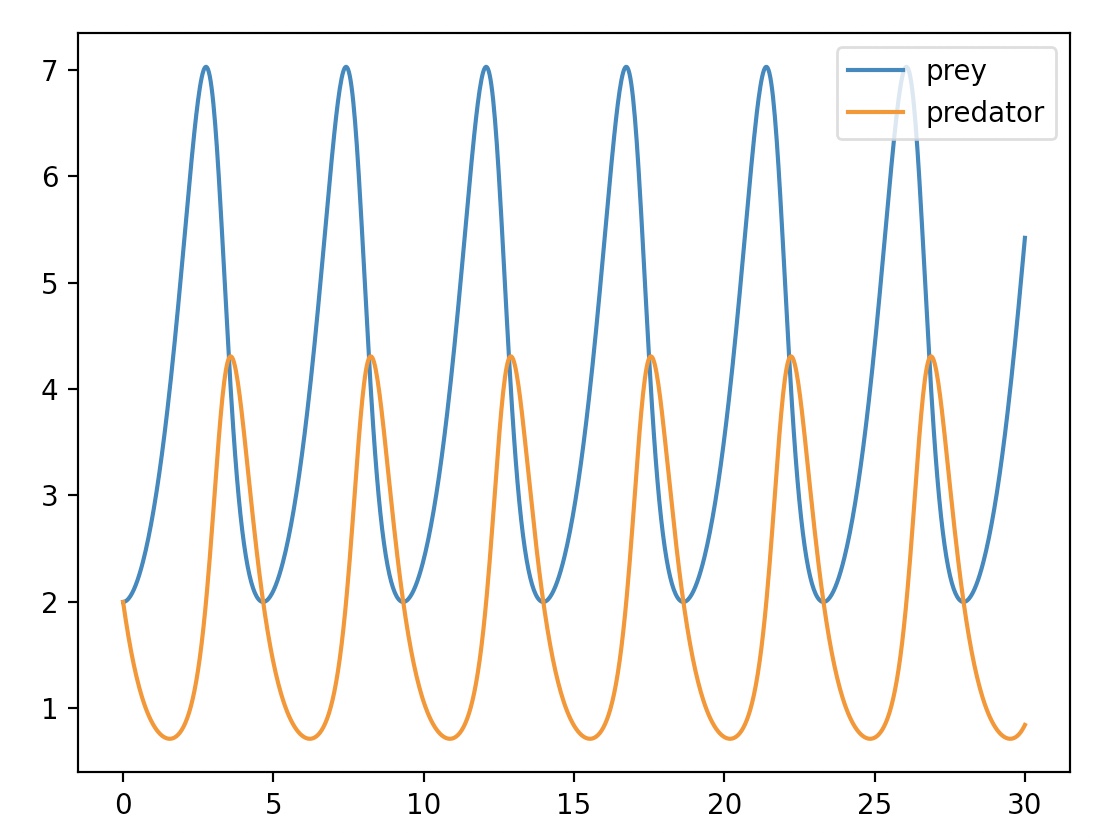
Lotka-Volterra equation
predator-prey equation
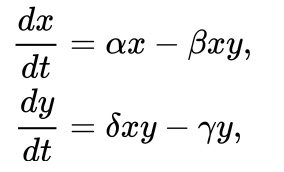x means prey, y means predator
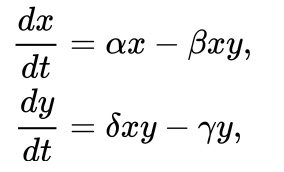x means prey, y means predatorwith alpha=1, beta=0.5, gamma=0.5, delta=2
initial condition x=y=2
from t=0, t=30
# Lotka-Volterra equation
# dx/dt=alphax-beta*x*y
# dy/dt=gamma*x*y-delta*y
import numpy as np
import matplotlib.pyplot as plt
def f(r, t): # dr/dt
x, y=r[0], r[1]
alpha=1; beta=0.5
gamma=0.5; delta=2
fx=alpha*x-beta*x*y
fy=gamma*x*y-delta*y
return np.array([fx, fy])
if __name__=="__main__":
t=np.linspace(0, 30, 1000)
dim=2
r=np.ones([len(t), dim])
k=np.zeros([4, dim], float) # Fourth Order Runge-Kutta Method
h=t[1]-t[0]
r[0][0]=2; r[0][1]=2
for i in range(1, len(t)):
k[0]=h*f(r[i-1], t[i-1])
k[1]=h*f(r[i-1]+k[0]/2, t[i-1]+h/2)
k[2]=h*f(r[i-1]+k[1]/2, t[i-1]+h/2)
k[3]=h*f(r[i-1]+k[2], t[i-1]+h)
r[i]=r[i-1]+(k[0]+2*k[1]+2*k[2]+k[3])/6
plt.plot(t, r[:, 0], label="prey")
plt.plot(t, r[:, 1], label="predator")
plt.legend()
plt.show()
